给定两个分布 p(z), q(z) ，它们可能在相同的变量 z 上定义，但其分布形状各异。两者之间的距离可以通过 相对熵 (Relative Entropy) 来度量，其定义如下：

D_{\text{KL}}(p \parallel q) = \sum_z p(z) \log \frac{p(z)}{q(z)}

或者在连续情形下为：

D_{\text{KL}}(p \parallel q) = \int p(z) \log \frac{p(z)}{q(z)} dz

其中：

1. 该指标衡量两个概率分布的差异，也被称为KL散度（Kullback-Leibler Divergence, KLD），以 Kullback 和 Leibler 的名字命名。
2. D_{\text{KL}}(p \parallel q) \geq 0 ，且当且仅当 p(z) = q(z) 时取值为0。
3. 它具有非对称性，即 D_{\text{KL}}(p \parallel q) \neq D_{\text{KL}}(q \parallel p) 。
4. 当 q(z) = 0 而 p(z) > 0 时， D_{\text{KL}}(p \parallel q) = \infty （无穷大）。
5. KL 散度并不是真正的距离度量，因为它不具备对称性，也不满足三角不等式。

直观理解：

KL散度在统计学和信息论中有着重要应用。它衡量了通过 q(z) 来近似 p(z) 时所引入的额外信息量。如果两者越接近，则KL散度越小，反之则越大。

反向 KL 散度与正向 KL 散度

KL散度有两种常见的计算方式：正向 KL 散度（Forward KL Divergence）与反向 KL 散度（Reverse KL Divergence）。它们有着不同的优化目标和物理意义。

1. 正向 KL 散度

正向 KL 散度定义为：

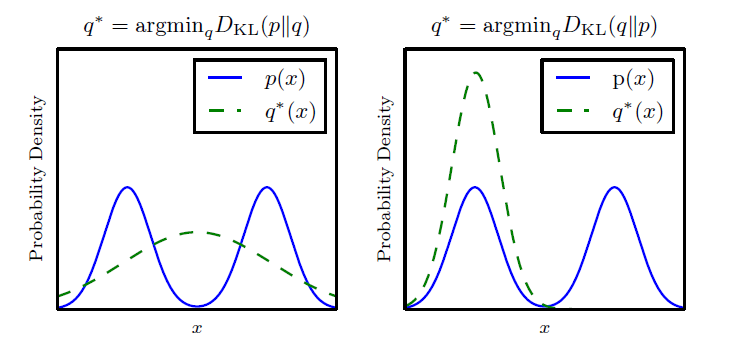
q^* = \arg \min_q D_{\text{KL}}(p \parallel q) = \arg \min_q \sum_z p(z) \log \frac{p(z)}{q(z)}

在优化过程中，我们希望找到一个分布 q(z) 来最好地逼近真实分布 p(z) 。从公式上看，正向 KL 散度强调 p(z) 的高概率区域，即逼近模型 q(z) 需要重点拟合 p(z) 可能性大的区域。

正向 KL 散度具有“zero forcing”的特性，意味着当 q(z) = 0 而 p(z) > 0 时，它会强制使散度趋向无穷大，从而推动 q(z) 分布覆盖到 p(z) 的所有高概率区域。这种逼近方式对于模型外推性要求高的任务非常重要。

2. 反向 KL 散度

反向 KL 散度定义为：

q^* = \arg \min_q D_{\text{KL}}(q \parallel p) = \arg \min_q \sum_z q(z) \log \frac{q(z)}{p(z)}

反向 KL 散度更关注分布 q(z) 的低概率区域，即它会惩罚 q(z) 在 p(z) 较低概率区域的非必要分布。这意味着反向 KL 散度更倾向于聚集到单一的区域，导致它在某些情况下产生过度的模式聚集。

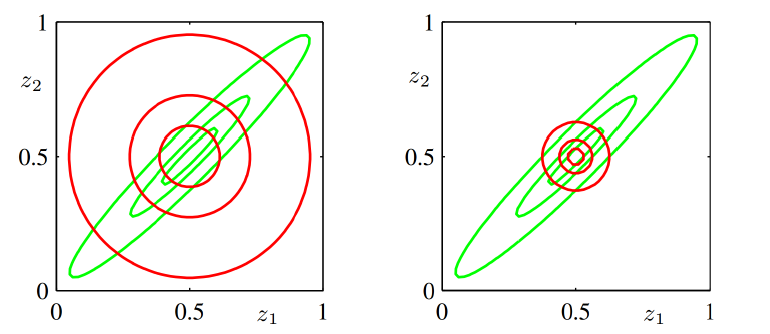
上图中绿色曲线代表真实分布 p 的等高线，红色曲线是使用近似 p(z_1, z_2) = p(z_1)p(z_2) 得到的等高线。
  • 左： D_{\text{KL}}(p \parallel q) ，正向 KL 散度，具有 “zero avoiding” 特性，导致分布更“宽”。
  • 右： D_{\text{KL}}(q \parallel p) ，反向 KL 散度，具有 “zero forcing” 特性，导致分布更“窄”。
此外，从上图也能看出，正向 KL 散度的分布会偏向一般化，而反向 KL 散度的分布会偏向特定化。
另一个问题是，如果我们令 p 是两个高斯分布的混合，而令 q 为单个高斯分布，那么两种 KL 散度如何选择呢？
由于正向 KL 散度和反向 KL 散度各自的特性，当 q 逼近 p 时，会出现下图的区别：
选择使用 KL 散度的方向取决于实际问题的需求，两者并没有优劣之分。某些应用需要近似分布 q 在真实分布 p 的高概率区域内也具有高概率，而另一些应用则需要 q 在 p 的低概率区域内保持低概率。选择 KL 散度的方向实际上反映了每种应用中我们优先考虑的特性。
上面左图展示的是最小化 D_{\text{KL}}(p \parallel q) 的效果。在这种情况下，我们选择一个 q ，使其在 p 高概率的区域也具有高概率。这意味着在优化过程中，我们更关注 p 中常见事件的准确性，也就是蓝线的双峰。我们希望确保在分布 q 中这些双峰不会变得过于罕见（即信息长度不至于过长）。当 p 有多个峰时， q 会倾向于将这些峰模糊处理，确保将高概率的质量分布在所有峰上。
右图展示的是最小化 D_{\text{KL}}(q \parallel p) 的效果。在这种情况下，我们选择一个 q ，使其在 p 的低概率区域也具有低概率。这意味着我们更在意 p 中罕见事件的处理，即蓝线的谷底，确保在分布 q 中这些罕见事件不会频繁出现（信息长度特别长的事件）。当 p 具有多个峰并且峰之间距离较大时，最小化反向 KL 散度的优化过程会倾向于选择一个单一的峰，以避免将概率质量分散到 p 的低概率区域之间。图中展示了 q 强调左侧峰时的结果，我们也可以选择右侧峰，得到相同的 KL 散度值。如果这些峰之间没有被明显的低概率区域分隔开，那么 KL 散度在此方向上可能依然会模糊多个峰。
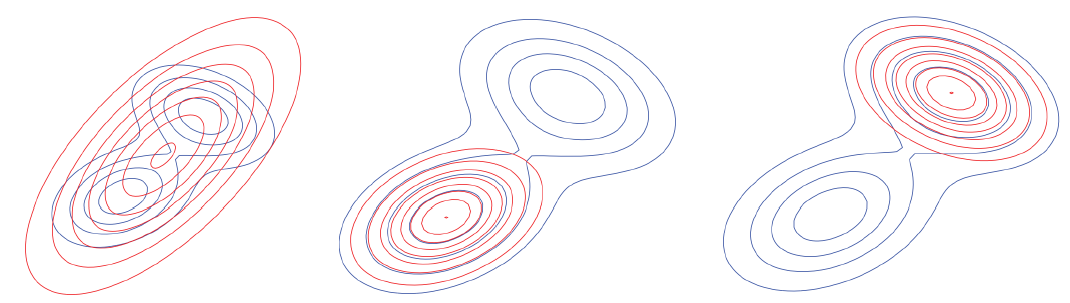
  • 左图：最小化 D_{\text{KL}}(p \parallel q) ，此时 q 趋近于完全覆盖 p 。
  • 中、右图：最小化 D_{\text{KL}}(q \parallel p) ，此时 q 能够锁定某一个峰值。