DPO的损失函数是什么,第一步的loss为多少?
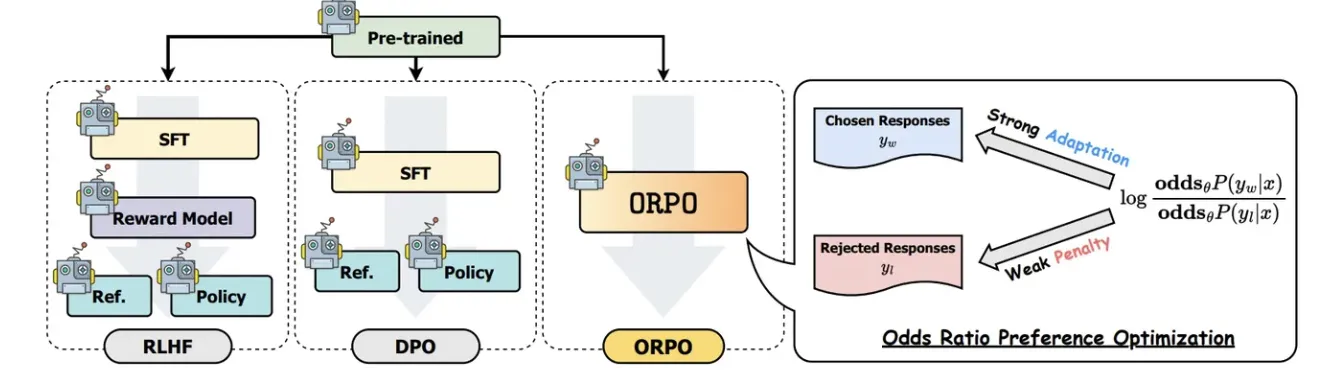
DPO的损失函数通常设计为最大化策略模型(即正在训练的模型)对偏好数据(chosen)和非偏好数据(rejected)之间的预测差异。具体来说,损失函数可以通过比较策略模型和参考模型(通常是冻结的,不参与训练)在偏好数据和非偏好数据上的预测得分来构建。参考模型的作用是在训练过程中提供一个稳定的基准,以确保策略模型的更新不会偏离太远。
\mathcal{L}_{\text{DPO}}(\pi_\theta; \pi_{\text{ref}}) = -\mathbb{E}_{(x, y_w, y_l) \sim \mathcal{D}}\left[\log \sigma\left(\beta \log \frac{\pi_\theta(y_w \mid x)}{\pi_{\text{ref}}(y_w \mid x)} - \beta \log \frac{\pi_\theta(y_l \mid x)}{\pi_{\text{ref}}(y_l \mid x)}\right)\right]
其中:
- \pi_\theta 表示策略模型,即正在训练的模型,其参数为 \theta。
- \pi_{\text{ref}} 表示参考模型,其参数在训练过程中保持固定。
- (x, y_w, y_l) \sim \mathcal{D} 表示从偏好数据集 \mathcal{D} 中随机抽取一个样本,其中 x 是输入提示语(prompt)
- y_w 是偏好的响应(chosen),y_l 是非偏好的响应(rejected)。
- \sigma 是Sigmoid函数,用于将输入转换为概率。
- \beta 是一个超参数,用于控制策略模型和参考模型之间差异的重要性。
根据公式,第一步 \pi_\theta == \pi_{\text{ref}} ,所以损失等于log2。