当前LLM的对齐过程通常分为SFT和RLHF两个阶段,我们是否有可能直接跳过SFT阶段而进入RLHF阶段?
可以。论文ORPO: Monolithic Preference Optimization without Reference Model,提出了一种称为ORPO的方法(Odds Ratio Preference Optimization),该方法将SFT和对齐融合到一个损失函数当中。
下图是RLHF、DPO、ORPO三种方法的比较。
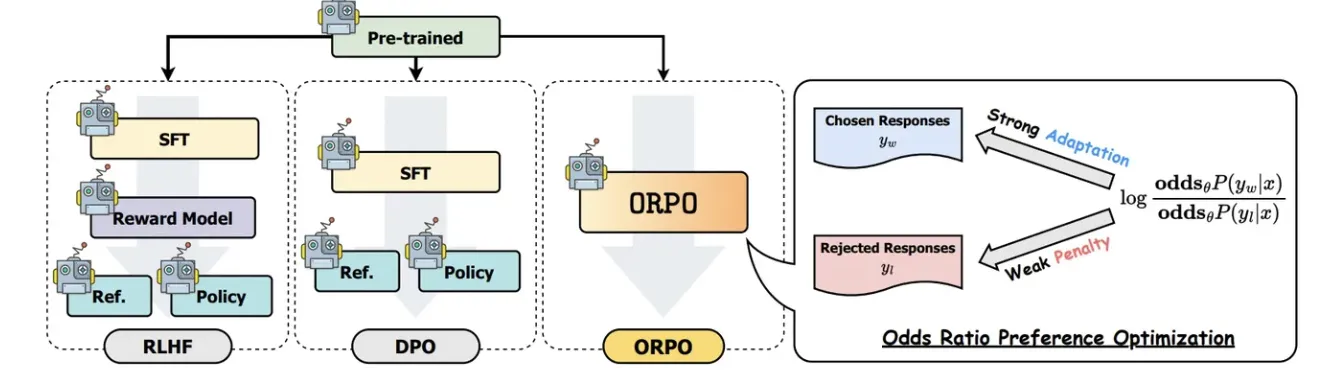
损失函数 L_{OR} 是 ORPO 算法的关键创新点,它通过几率比(Odds Ratio)来区分优选响应(chosen responses)和非优选响应(rejected responses)几率比 OR_{\theta}(y_w, y_l) 定义为优选响应 y_w 和非优选响应 y_l 相对于输入 x 的几率之比:
OR_{\theta}(y_w, y_l) = \frac{\text{odds}_{\theta}(y_w | x)}{\text{odds}_{\theta}(y_l | x)}其中, \text{odds}_{\theta}(y | x) = \frac{P_{\theta}(y | x)}{1 - P_{\theta}(y | x)} 是在给定输入 x 下生成序列 y 的几率.
L_{OR} 的目标是最大化 y_w 和 y_l 之间的几率比,通过在损失函数中加入一个简单的对数几率比项来实现:
L_{OR} = -\log \sigma \left( \log \frac{P_{\theta}(y_w | x)}{1 - P_{\theta}(y_w | x)} - \log \frac{P_{\theta}(y_l | x)}{1 - P_{\theta}(y_l | x)} \right)其中, \log \sigma 是对数sigmoid函数,用于将对数几率比转换为一个可优化的损失项。
ORPO的总损失函数是 L_{SFT} 和 L_{OR} 的加权和,其中 \lambda 是一个权重参数,用于平衡两部分损失:
L_{ORPO} = \mathbb{E}(x, y_w, y_l) [L_{SFT} + \lambda \cdot L_{OR}]


