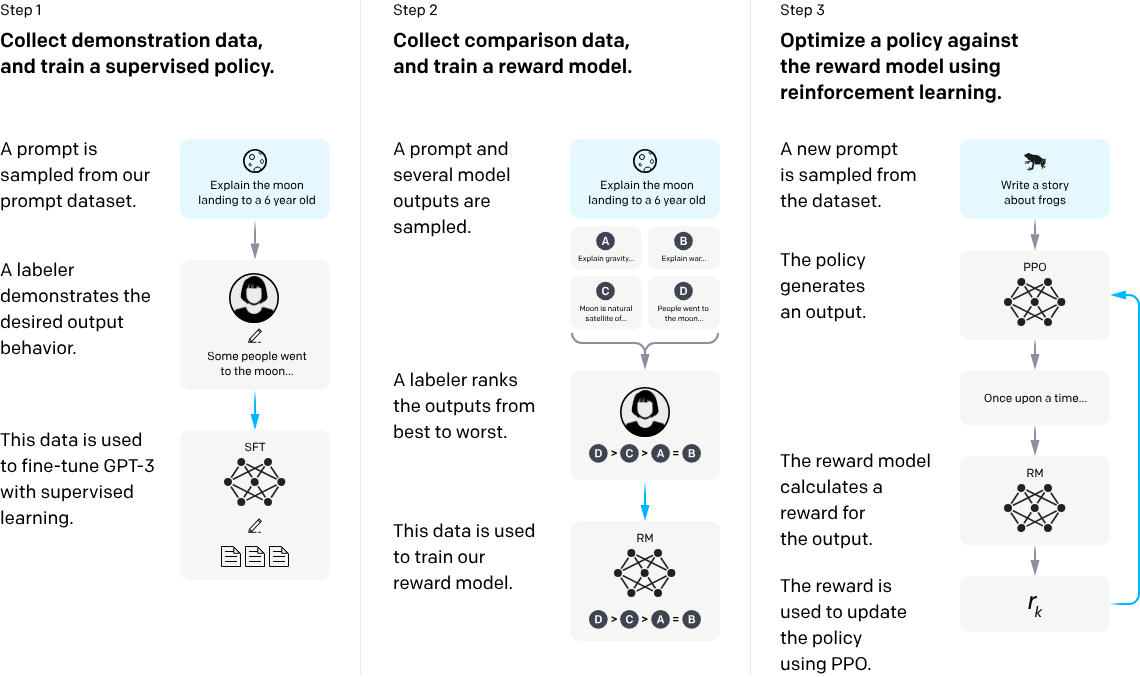
优势是什么
在强化学习(Reinforcement Learning)中,优势函数(Advantage Function) 是一个非常重要的概念。优势函数衡量了某个动作相对于其他动作的好坏程度,具体来说,它表示在某个状态下采取某个动作,是否比平均策略中的其他动作表现更好。优势函数通常定义为:
A(s, a) = Q(s, a) - V(s)
其中, Q(s, a) 是在状态 s 下采取动作 a 的动作-价值函数(Action-Value Function),而 V(s) 是状态 s 的状态-价值函数(State-Value Function)。直观上,优势函数反映了当前动作相对于该状态下平均策略动作的“优势”程度。如果优势函数为正,说明这个动作比平均情况要好;为负,则说明不如其他动作。
在策略优化中,计算优势函数的好坏直接影响到策略的更新。因此,如何准确高效地估计优势函数至关重要。
用蒙特卡洛方法估计优势
蒙特卡洛方法 是估计优势函数的一种方式。蒙特卡洛方法通过对完整的轨迹进行采样,计算实际的回报来估计价值函数。具体地,利用从状态 s 到回合结束的总回报来估计 Q(s, a) ,然后再用:
A(s, a) = R(s, a) - V(s)其中, R(s, a) 是从状态 s 采取动作 a 后获得的实际总回报。通过这种方式,我们可以得到一个无偏的优势估计。
然而,蒙特卡洛方法的缺点也非常明显。首先,它依赖于回合的完整性,只有在整个回合结束后才能得到估计结果,因此不能用于在线场景。其次,它的方差较大,因为单次采样可能会受到偶然因素的影响,因此估计结果可能不稳定。
用时序差分法估计优势
与蒙特卡洛方法不同,时序差分(Temporal Difference, TD)方法是一种利用一步预测来估计价值函数的方式。时序差分法通过结合当前时刻的估计值和下一个状态的估计值来更新当前的价值估计。对优势函数的估计可以用以下公式表示:
A(s, a) = r + \gamma V(s') - V(s)其中, r 是当前状态 s 采取动作 a 所得到的即时奖励, \gamma 是折扣因子,而 V(s') 是下一状态 s' 的价值。
时序差分方法相比蒙特卡洛方法有一些优点。首先,它可以在不需要等待整个回合结束的情况下进行更新,因此适合在线学习。其次,它的估计结果方差较小,因为它依赖于多个小步的估计,平滑了每一步的波动。
然而,时序差分方法也有局限性。它虽然降低了方差,但由于使用了估计的价值来更新,可能会引入一些偏差。因此,如何在偏差和方差之间进行权衡,是估计价值函数时需要考虑的问题。
广义优势估计
广义优势估计(Generalized Advantage Estimation, GAE) 是一种结合蒙特卡洛方法和时序差分方法优势的估计方式。它通过引入一个混合系数 \lambda 来在偏差和方差之间进行灵活调节。GAE的核心思想是利用多个时序差分(TD)步骤的加权和来估计优势,从而在保证方差较低的同时,尽量减少偏差。其定义为:
A^{GAE}_t = \sum_{l=0}^{\infty} (\gamma \lambda)^l \delta_{t+l}其中, \delta_t = r_t + \gamma V(s_{t+1}) - V(s_t) 是时序差分误差,而 \lambda 是权衡偏差和方差的参数。当 \lambda = 1 时,GAE退化为蒙特卡洛方法,方差较大但无偏。当 \lambda = 0 时,GAE退化为时序差分方法,偏差大但方差较小。
接下来我们介绍一下 GAE 的推导过程。首先,用 \delta_{t} 表示时序差分误差,其中 V 是一个已经学习的状态价值函数。于是,根据多步时序差分的思想,有:
\begin{array}{ll} A_{t}^{(1)}=\delta_{t} & =-V\left(s_{t}\right)+r_{t}+\gamma V\left(s_{t+1}\right) \\ A_{t}^{(2)}=\delta_{t}+\gamma \delta_{t+1} & =-V\left(s_{t}\right)+r_{t}+\gamma r_{t+1}+\gamma^{2} V\left(s_{t+2}\right) \\ A_{t}^{(3)}=\delta_{t}+\gamma \delta_{t+1}+\gamma^{2} \delta_{t+2} & =-V\left(s_{t}\right)+r_{t}+\gamma r_{t+1}+\gamma^{2} r_{t+2}+\gamma^{3} V\left(s_{t+3}\right) \\ \vdots & \vdots \\ A_{t}^{(k)}=\sum_{l=0}^{k-1} \gamma^{l} \delta_{t+l} & =-V\left(s_{t}\right)+r_{t}+\gamma r_{t+1}+\ldots+\gamma^{k-1} r_{t+k-1}+\gamma^{k} V\left(s_{t+k}\right) \end{array}然后, GAE 将这些不同步数的优势估计进行指数加权平均:
\begin{aligned} A_{t}^{G A E} & =(1-\lambda)\left(A_{t}^{(1)}+\lambda A_{t}^{(2)}+\lambda^{2} A_{t}^{(3)}+\cdots\right) \\ & =(1-\lambda)\left(\delta_{t}+\lambda\left(\delta_{t}+\gamma \delta_{t+1}\right)+\lambda^{2}\left(\delta_{t}+\gamma \delta_{t+1}+\gamma^{2} \delta_{t+2}\right)+\cdots\right) \\ & =(1-\lambda)\left(\delta\left(1+\lambda+\lambda^{2}+\cdots\right)+\gamma \delta_{t+1}\left(\lambda+\lambda^{2}+\lambda^{3}+\cdots\right)+\gamma^{2} \delta_{t+2}\left(\lambda^{2}+\lambda^{3}+\lambda^{4}+\cdots\right)+\cdots\right) \\ & =(1-\lambda)\left(\delta_{t} \frac{1}{1-\lambda}+\gamma \delta_{t+1} \frac{\lambda}{1-\lambda}+\gamma^{2} \delta_{t+2} \frac{\lambda^{2}}{1-\lambda}+\cdots\right) \\ & =\sum_{l=0}^{\infty}(\gamma \lambda)^{l} \delta_{t+l} \end{aligned}其中, \lambda \in[0,1] 是在 GAE 中额外引入的一个超参数。当 \lambda=0 时, A_{t}^{G A E}=\delta_{t}=r_{t}+\gamma V\left(s_{t+1}\right)-V\left(s_{t}\right) , 也即是仅仅只看一步差分得到的优势; 当 \lambda=1 时, A_{t}^{G A E}=\sum_{l=0}^{\infty} \gamma^{l} \delta_{t+l}=\sum_{l=0}^{\infty} \gamma^{l} r_{t+l}-V\left(s_{t}\right) , 则是看每一步差分得到优势的完全平均值。
为方便计算,GAE可以通过递推形式计算。我们通过对 A^{GAE}_t 进行展开,可以得到以下递推公式:
A^{GAE}_t = \delta_t + (\gamma \lambda) A^{GAE}_{t+1}这种递推形式使得计算 GAEs 只需一次向前遍历数据,不需要累积全部未来奖励,从而大大提高了计算效率。
代码:
def compute_advantages(
self: torch.FloatTensor,
values: torch.FloatTensor,
rewards: torch.FloatTensor,
mask: torch.FloatTensor,
):
lastgaelam = 0
advantages_reversed = []
gen_len = rewards.shape[-1]
values = values * mask
rewards = rewards * mask
for t in reversed(range(gen_len)):
nextvalues = values[:, t + 1] if t < gen_len - 1 else 0.0
delta = rewards[:, t] + self.config.gamma * nextvalues - values[:, t]
lastgaelam = delta + self.config.gamma * self.config.lam * lastgaelam
advantages_reversed.append(lastgaelam)
advantages = torch.stack(advantages_reversed[::-1]).transpose(0, 1)
returns = advantages + values
advantages = masked_whiten(advantages, mask)
advantages = advantages.detach()
return values, advantages, returns
广义优势估计的好处主要体现在以下几个方面:
1. 降低方差:通过时序差分多步估计,GAE的估计比纯蒙特卡洛方法稳定,避免了单次采样导致的方差过大。
2. 减少偏差:与时序差分方法相比,GAE通过混合多个时间差分估计,减少了过度依赖短期估计所带来的偏差。
3. 适用性强:GAE既可以用于批量学习场景,也可以在在线学习中应用。它的灵活性使其成为策略梯度算法(如PPO)的常用选择。
4. 性能提升:在实际强化学习任务中,GAE可以加速收敛并提高策略优化的效率,特别是在复杂的任务环境中表现出色。
总体来说,广义优势估计通过引入 \lambda 参数,有效地在偏差和方差之间找到了平衡点,成为强化学习中广泛应用的估计方法之一。